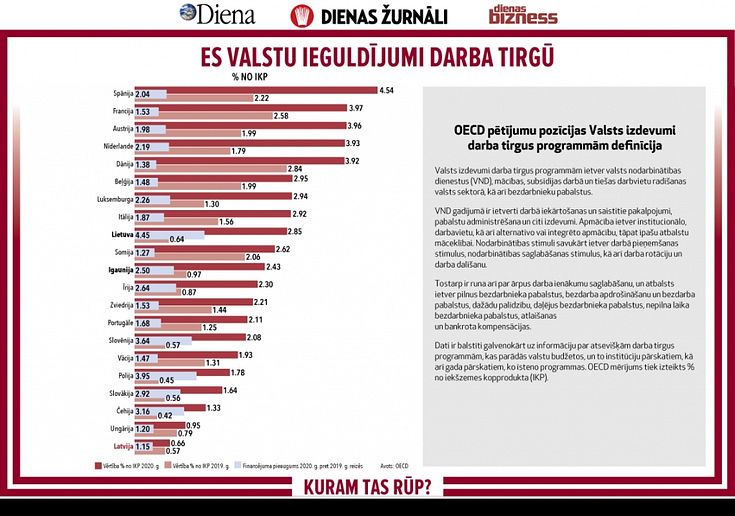
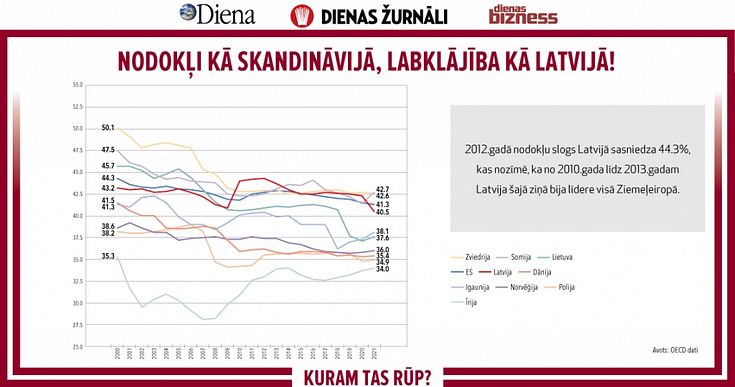
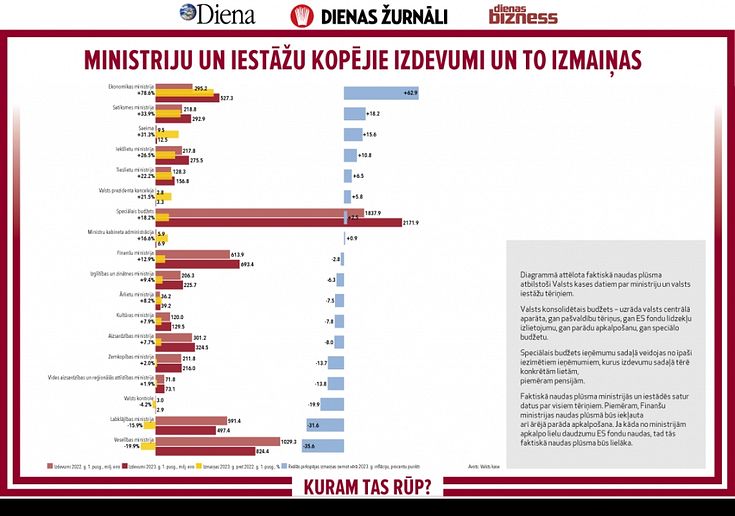
Par to, ka vairumam bērnu vairs neinteresē fizika, ķīmija, bioloģija, kas vēlāk traucē studēt eksaktās augstskolās, vairs nav šaubu. Iniciatīvas grupa Kuram tas rūp? izvirza pieņēmumu, ka ķezas pamatcēlonis nav dabaszinību mācīšanas metodikā vai saturā, bet gan pamatskolas matemātikas mācīšanā un apguvē.
Nevar salīdzināt zināšanu pārbaudes
Mēs varētu analizēt matemātikas pārbaudes darbus desmitgažu garumā, tomēr izglītības programmas ir mainījušās un, kā norādīja Izglītības un zinātnes ministrijas Sabiedrisko attiecību daļā, dati nav salīdzināmi. Pēc sarunām ar vairākiem pamatskolas pedagogiem jāatzīst, ka tiešām nav iespējams salīdzināt rezultātus, jo trīs desmitgažu garumā pārbaudes darbu prasības ir padarītas aizvien vienkāršākas.
Proti, jau sen nav mutvārdu eksāmena ģeometrijā, no matemātikas pārbaudes darbiem trīs desmitgažu laikā ir izzudusi virkne teksta uzdevumu un salīdzināt atrisināto uzdevumu daudzumu patiešām būtu galēji aplami. Mūsu paraugam ņēmām tikai pēdējos datus par 2021./2022. mācību gada matemātikas pārbaudes darbiem 6. un 9. klasē. Dati par vidējiem skolēnu rezultātiem, kā arī paši uzdevumi atrodami IZM interneta vietnē, kurus katrs var analizēt arī patstāvīgi.
6. klase – klupšanas akmens procenti un proporcijas
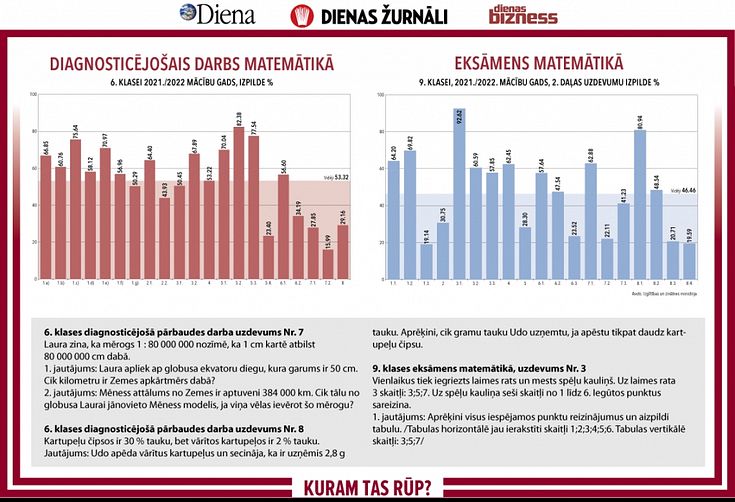
Diagnosticējošais darbs matemātikā 6. klasei parāda ārkārtīgi zemus rezultātus trīs piemēru gadījumā, divos saistītos uzdevumu tipos. Pirmajā uzdevumā Nr. 7 dots globusa mērogs, jāaprēķina ekvatora garums dabā, ja zināms ekvators uz globusa, – atrisinājuši 27,85% skolēnu. Tas pats mērogs, jautājums – cik tālu no globusa jānovieto mēness modelis, ja zināms tā reālais attālums no zemes. Atrisinājuši 15,99% skolēnu. Abos uzdevuma piemēros ir runa par proporciju rēķiniem, kurus māca 6. klasē. Nelaime, visticamāk, slēpjas apstāklī, ka proporciju uzdevumus nevar pasniegt citādi kā vien teksta formā. Iespējams, ir otra problēma, trūkst uzdevumu vizualizācijas risinājumu un skolēni tā arī nesaprot proporcionalitātes jēgu.
Proti, ja nav sajēgas par terminiem trijstūrī, nav iespējams saprast, vai divi trijstūri ir proporcionāli. Otrs uzdevums ir procentus saturošais uzdevums Nr. 8, kas paredz divpakāpju risinājumu. To atrisinājuši 29,16% skolēnu. Šo uzdevumu risināšanu nevar metodiski saistīt ar proporciju rēķiniem, lai arī procentu uzdevumi pēc būtības ir proporciju uzdevumu speciāls gadījums. Tā vietā, lai iemācītu saprast, šo uzdevumu rēķināšana ir metodiski nodalīta no pamatjēgas – proporcijām. Viena universāla paņēmiena vietā, kas dotu sapratni par visa veida procentu uzdevumiem, skolotāji nepaguruši māca iegaumēt trīs formulas, kur katra atbilst kādam no trim iespējamajiem nezināmajiem. Nav zināms procents no lieluma – viena formula, nav zināma lieluma daļa, bet zināms procents, otra formula, nav zināms lielums, trešā formula. Formulas bērniem ir zināmas, bet atrisināmības procents ir zemāks par minēšanas metodi. Proti, ja skolēni minētu, tad pareizo atrisinājumu būtu vismaz 33%.
9. klase – 7,4% neprot reizrēķinu!
9. klases eksāmenu darbā skaidri parādās, ka trešdaļai skolēnu nav skaidrības par matemātiskiem jēdzieniem – par to, kas īsti ir kvadrāts, kas rombs, kuras trijstūra malas definē sinusu, kuras kosinusu utt. Proti, ģeometrijas noniecināšana, to neizdalot kā atsevišķu disciplīnu, ir ar sekām. Ja skolēns nesaprot laukuma jēdzienu, ir grūti sagaidīt, ka būs sapratne par kvadrāta jēdzienu algebrā. Var izvirzīt pieņēmumu, ka vairāk nekā trešdaļai skolēnu pieklibo plaknes un telpas jēdzienu izpratne vai arī nav spējas reizināt un dalīt naturālus skaitļus. Proti, šaubas rodas arī par pirmajās četrās klasēs apgūto vai vēlāk nenostiprināto.
Daudzos no uzdevumiem nojaušams, ka bērni neprot interpretēt tekstu matemātiskos terminos, lai kaut nonāktu uz pareizā ceļa risinājumā. Eksāmens 9. klasē ir sadalīts divās daļās, un, ja pirmajā daļā, kas ir samērā vienkārša, vidējais atrisināmības rādītājs ir 61,1%, tad otrajā kopumā ir daudz sliktāk. Šeit drīzāk uzsvērti jānorāda uz to, ko skolēni veiksmīgi izdarījuši. Piemēram, veiksmīgi ir atrisināta nevienādība ar mainīgo, atrastas kvadrātvienādojuma saknes, kur runa ir par skaitļu ievietošanu priekšā uzrakstītā formulā skolēnu lapā. Izcili labi ir klājies ar vienciparu naturālu skaitļu reizināšanu – 92,6% pareizu atbilžu.
Skumjā sadaļa, ka paliek 7,4%, kuri 9. klasi beidzot, nezina reizrēķinu, turklāt viņiem nav pacietības vai priekšstata, ka, nezinot pareizo atbildi, var arī, piemēram, piecreiz saskaitīt skaitli septiņi. Tajā pašā uzdevumā, otrajā daļā, ir jautājums par dalāmību ar 6 un pozitīvo atbilžu ir par 30% mazāk, kas norāda, ka bērni nav gana trenēti galvas rēķinos un, lai arī prot reizināt, nevar sadalīt reizinātājos. 81% skolēnu prot konstruēt funkciju grafikus. Līdzko jākonstruē līknei piederošs simetrisks punkts, pozitīvu atbilžu ir par 30% mazāk. Visticamāk, ka liela daļa no aplamām atbildēm ir tāpēc, ka bērni nesaprot jēdzienu simetrisks koordinātu plaknē vai arī vispār neizprot simetrijas jēdzienu pēc būtības.
Formulas vai prasme domāt
9. klases pārbaudes darba laikā ir iespēja izmantot formulu lapu. Proti, skolotāji deviņus gadus centīgi dzinuši bērnu galvās formulu pielietojumu, tās eksāmenā ir noliktas acu priekšā un tomēr rezultāti ir slikti. «Skolēnam netiek parādīts matemātikas princips. Tā vietā tiek iemācīts, kā aprēķināt piemēru, bet skolēns nezina, ko darīt, ja piemērs tiek kaut nedaudz mainīts. Daudzu nelaimju sakne jau ir sākumskolā, kur netiek ielikti būtiski pamati. 7. klasē redzams, ka tekstpratība ir slikta. Skolēni neprot nolasīt informāciju arī no vienkāršām infografikām, kas īpaši izstrādātas, lai būtu vieglāk uztveramas,» atzīst matemātikas skolotāja Egija. Proti, problēmas ir zināmas, tomēr nevar atzīt, ka mūsu bērni matemātiku neapgūst. Lielākais vairums! Daļa apgūst pietiekamu skaitu formulu pielietojumu atpazīstamos uzdevumos, bet ne matemātikas priekšmetu. Ja šodienas skolēniem lūgtu nolikt pamatskolas eksāmenu matemātikā, kuru kārtojuši bērni pirms 30 gadiem, nesekmīgo būtu krietni vairāk par pusi.
Ietekme uz dabaszinātnēm
No aprakstītajām kļūdām skolēnu darbos var izdalīt atsevišķas tēmas, kuras, sākot apgūt dabaszinātnes – fiziku, ķīmiju, bioloģiju, ir kritiski nepieciešamas. Pirmkārt, reizināšana, darbības ar daļām, sadalīšana pirmreizinātājos, lielākā kopīgā dalītāja atrašana utt., ir jebkuras dabaszinātnes uzdevumu pamatā. Neorganiskajā ķīmijā, lai uzrakstītu ūdens reakciju, piemēram, ar sērskābi, būs jāprot veikli darboties ar naturāliem skaitļiem un veikt pieminētās darbības. Ja šīs prasmes nav, interesanta skolēnam var būt vien tā ķīmijas stundas daļa, kurā skolotājs demonstrē kādu eksperimentu vai stāsta par vispārīgām lietām, bet uzdevumu risināšana viņam izraisīs riebumu un protestu, jo viņš tos nekādi nevar atrisināt!
Tāpat fizikā ir būtiskas prasmes darbībās ar naturāliem skaitļiem, izpratne par darbībām ar pakāpes rādītājiem, bez kā nav iespējama mērvienību pārveidošana, utt. Lielākā daļa no šīm zināšanām tiek apgūtas pirmajās sešās klasēs. Proporcijas un procenti ir īpaši izceļami, jo dabaszinātņu pārbaudes darbos bez šī elementa neiztiek. Proporcijas un procenti dažādos bioloģijas, fizikas un ķīmijas uzdevumos sastopami aptuveni piektdaļā gadījumu, un tieši šie uzdevumi netiek atrisināti visvairāk. Šo secinājumu izdaru no laika, kad pats mācīju fiziku pamatskolā. Ievērojot, ka kopš tā brīža ir pagājuši 20 gadi, iespējams, ka procentu un proporciju īpatsvars dabaszinātņu pārbaudes darbos ir jau samazināts, tomēr dabā, praktiskajā dzīvē – bez matemātikas prasmēm nevar risināt nevienu dabaszinātņu uzdevumu.
Piemēram, visi šķidrumu jaukšanas uzdevumi prasa tieši proporciju uzdevumu sapratni. Proti, apgalvojums, ka vidusskolas nespēj sagatavot jēdzīgus inženierzinātņu un eksakto zinātņu studentus, ir patiess, bet vaina pirmām kārtām nav jāmeklē vidusskolā. Pamats ir sākumskolā un, iespējams, vēl pirmsskolā, jo arī uzmanības trūkumam un hiperaktivitātei ir savi cēloņi. Šīs parādības nav kāda īpaša Z vai A paaudzes īpašība, bet tikai dažu aplamu audzināšanas un ēdināšanas paradumu sekas, kas mazo bērnu sadzīvē ir izsakāms trīs vārdos – mazkustība, ekrāns, cukurs. Šoreiz noslēguma jautājums skan šādi: «Kuram izglītība rūp no paša sākuma līdz beigām?»